�����̑o���`���ɂ��āi�P�j�@�@���̂Q�@�̑����B
�z���w�ɂ����o��(�p twin, �� Zwilling)�́A�����A�l�̑o�q�i�o�����F�c�C���j���C���[�W�����p��ł���B�o�q�͕�e�̂������瓯�����ɑ������Ő��܂ꂽ�q�ŁA�q���̍������l���������������̎p�`�����Ă��邱�Ƃ������B�V���u�L�����v(1979��)�������ƁA�u�ꗑ���Ɠ��Ƃ���A��҂͓����̂��Ƃ��ِ��̂��Ƃ����邪�A�O�҂͕K�������B�v�Ƃ���B
�����őo���́A��̓����p�`�̌����i�́j��������Ő����Ă�����́A�������Ɂi�����j���j�������āA���������̎��������Đ����������̂����C���[�W�ƌ�����B�����l�Ԃ̑o�q�͕��ʁA�Ɨ������ʁX�̑̂������Đ��܂�Ă��邪�A�z���̏ꍇ�͓�̌̂��������Ă���i���邢�͘A�ꍇ���Ă���j�ꍇ�Ɍ����đo���ƌĂԁB
����������ƁA��̎n���o���j�̑��݂��O��Ƃ��ĉ��肳��A���̊j����o�����X�̂Ƃꂽ�����I�������o�āA�������̓��m���w�I�ȊW�Ōq�����Č�������̂��Ă̂��n�܂�ƌ����悤�B�Ⴆ�A��e�̑ٓ��ɋ[���������ɁA�����̌����j�������ɐ����āi�Ɖ��肵�āj�A�̂Ƃ��ē����p�`�ɐ������ēƗ��ɕ���ł����Ƃ��Ă��o���Ƃ͌Ă�Ȃ��B
�����������C���[�W���炷��ƁA�傫����p�`�̒������قȂ��̌̂������\����̑o���W�Őڍ����Ă��Ă��A�o���ƌĂׂȂ��Ƃ���l�����ɂ͈ꗝ����B��̑傫�Ȍ̂̕\�ʂɁA�ʂ̌̂��I�ɔz���I�ɕt���������̂��R�肾�낤�Bcf.
No.1007 ��L�P
����A�����̑o���Ƃ��ĕ��ՓI�Ȃ̂͋������i�u���W������h�t�B�[�l���j�����A���̃z���E�^�C�v�͌`�ԓI�ɂقڒP�����ƕς�炸�A�܂�őo�q�ɂ͌����Ȃ��B�w�e���E�^�C�v�ł���X�����ł��A�g�̎��`�����`�O�A�Ȃǂ̕s�ύt�Ȍ`�Ԃ̂��̂͂�͂茴�C���[�W����O���B������������o���łȂ��Ǝ咣���錋���w�҂͍����܂����Ȃ����낤�B
�o���̒�`������ƂƂ��ɕω�����B�w���̔����ȗ��A�����̍\����Ώ̐������q���x���ŗ����o����悤�ɂȂ������A�܂��o���p�^�[���͖ڂɌ����Ȃ����x���̔����̈�ɂł����ʂɁi�J��Ԃ��j���݂��邱�Ƃ��m����悤�ɂȂ����B�o���͕K���������o�I�ɖ��ĂȌ`�Ԃ�Ȃ��ꍇ�ɂ��K������T�O�ƂȂ��Ă���̂��Bcf.
No.1005(�o���̒�`)
�����ɑΏ����i�E��^�ƍ���^�Ɓj�����邱�Ƃ� 19���I����m���Ă����B��҂����������o���`�Ԃ́A�^�̈Ӗ��ł̑o�����ǂ����A���鎞���ɂ͐^���ȋc�_���������B�ÓT�����w�̌n���́A�Â� N.�X�e�m�A�����E�h�E���[���AR-J.�A���C�AC.S.���C�X��̐��I�������o�āA20���I���O��ɍ��������}�����BV.�S�[���h�V���~�b�g(1853-1933)�͓����̑�\�I�Ȋw�҂̈�l���������A�o���̒�`�Ɉ�ƌ����f���A�Ώ��̂̐ڍ��ɂ��Ă��J��Ԃ��_�����B���̖��͂������A�����I�ɂ͓��i�A���_��^����K�v�̂Ȃ��g�s�b�N�̂悤���B
���Ȃ݂Ɏs��̊Ò��̖ڂ��炷��ƁA�X�����̑o���͉E��^���m�ior
����^���m�j�ł��낤�ƁA�E��|����^�ł��낤�ƁA���C���[�W�ɏƂ炵�đo���ȊO�̂Ȃɂ��̂ł��Ȃ��B�`���A�L�����Ɉ������悤�ɁA�Ⴂ�͈ꗑ���������i�������ِ����j�̔��e�ɗ��܂��Ă���B
�����āA�o���̎�ނ̘b�ɖ߂낤�B
V.�S�[���h�V���~�b�g�� 1898�N�ɔ��\�����u�o���̒�`�ɂ��āv(Über Definition eines Zwillings)�ŁA��q�̌��C���[�W���܂߂Ē�`�������A��̗�Ƃ��Đ����́u��ʂɑo���ƌĂ��R��ނ̋K���I�Ȗ����v��_�����B ���̂R��� Dana �̍z���̌n 6th(1892)�ɐ}�łŏЉ�ꂽ�i���z�j�`��ł���B
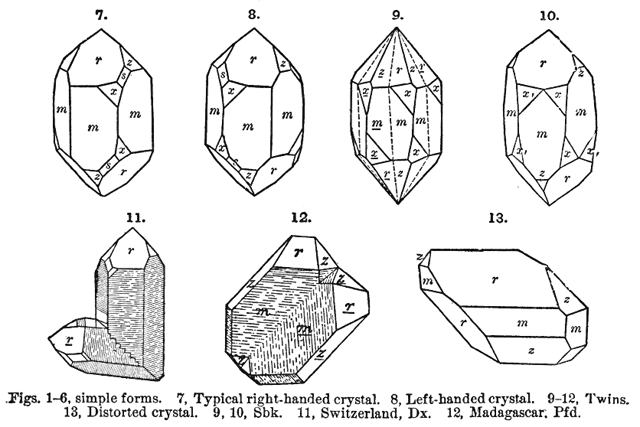
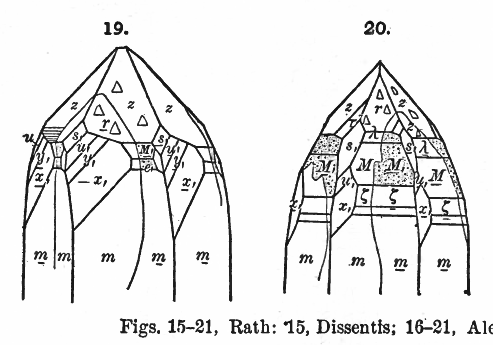
J.D.Dana�̖��������� The System of Mineralogy�@6th
(1892)�@���
�}9, 10 �͂�����݂̗�̗��z�}
����͎厲�������鍶�E�Ώ����̌̓��m�̖����ŁA���������u���W����(�}10)�B
����͎厲�������铯���^�̌̓��m��
60����]�����z�u�ł̖����ŁA���������h�t�B�[�l��(�}9,19,20)�B
�����đ�O��͍��������̖ʂ�o���ʂƂ���X����-�K���f�b�g���i���{���j�i�}11,12)�B
���̎����̃S�[���h�V���~�b�g�́A�P�ƂQ�Ƃ͖��炩�Ɂu�o���v�̒�`����O��Ă���i�����͎��ɂ͂悭�����o���Ȃ����j�A�R�͗��ۏ����t�������u�o���v�ƌĂׂ�ƍl�����B
�ނ͂��̌���������d�˂āA�u�����̑o���`���ɂ��āv(Über die Zwillingsgesetze des Quarz: 1905�N�j�ŁA���������ꂽ�\���Œ�`���q�ׂ��B���̘_���Ō��y���ꂽ�o���`���� No.938�ŐG�ꂽ���A�Čf����ƁA
�T�F�o���̎厲�ic���j�����s�Ȃ��́c���������u���W�����o�`�Da)�E��^�{����^�p�A
�@�@�y�уh�t�B�[�l���o�a�Db)�E��^�{�E��^�A
c) ����^�{����^�A d)�E��^�{����^�p
�@�@�̂Q��i�S�^�C�v�j�B
�U�F�o���̎厲�ic���j���X���Ă�����́c���̂R��
C: ���{���iC.S.���C�X���j
D: ���C�w���V���^�C��-�O���[�[�����^�[����
E: �T���W�j�A���@
�ł���B
���̂P�ŏЉ���f�N�����]�[�̋L�q��A���̂Q�ŏЉ���C�F���V���̋L�q�Ɣ�r����Ɩ��炩�����A�b�̌`���͏]���K���f�b�g���A���C�X���Ȃǂƌď̂���Ă������̂��B��������{�Y�����B�W�{�s��ɂ悭����Ă����Ƃ������R�œ��{���ƌĂi�K���f�b�g�����悭����Ă����͂������j�B
�c�̌`���͏]�����C�w���V���^�C�����ƌĂꂽ���̂ŁA��������̂�ς����B
�d�̌`���͔����I�O�̃Z�b���̕�(1856�N)�ȗ��A���Ⴊ�Ȃ��������A�m���Ƃ݂��悤���B�������A�c�Ƃd�Ƃ��ɂ߂Ē������`���ł��邱�Ƃ͌J��Ԃ��f���Ă����i�c�̎���̓��[�[�ƃS�[���h�V���~�b�g�̌v�Q���A�d�̓Z�b���̂P���̂݁j�BC,D,E�̖��͈̂ȍ~�قڒ蒅�����ς�����B
����A�C�F���V�����������`�������h���ƃc���B�b�J�E���ɂ��ẮA���R�̎Y���i���ʂ̖����j�ł��邩�Ɉ����āA�U��Ɋ܂߂Ȃ������B
�Ƃ͂����A�قǂȂ��S�[���h�V���~�b�g�̓u���C�g�n�E�v�g�����邢�̓c���B�b�J�E���Ɏ����`���̑o���W�{�ׂ�@��������A�V���ȌX���p�x������o�����B�ނ͂�����c���B�b�J�E���ƍl���āA���̎��݂�M�����B
1908�N�́u�����ɂ��āv( Über Quarz
�j�ł́A�V�D�w�e���E�c�C���̃O���[�v��݂��āA
F. �c���B�b�J�E���i�C�F���V���j
G.�`�������h���i�C�F���V���j
���L�ڂ���B���łɌ����ƁA �U. D�� R-�c�C���i�H�ʑ̖ʂ�o���ʂƂ�����́j�ƌĂсA(i)
�O���[�[�����^�[���E�^�C�v�� (ii)
���C�w���V���^�C���E�^�C�v�Ƃɕ������B
F. G. �̗��҂́A���N���
F.�V���f�����X�C�X�Y�ɕ����̎�������i���}�j�B
�V���f���͂܂��A�S�[���h�V���~�b�g���c���B�b�J�E���Ƃ݂��i�X���p�x�����قȂ�j����A�V������`���Ɣ��f���ăS�[���h�V���~�b�g���ƌĂB
��V.�S�[���h�V���~�b�g�͎���i�W�{�j�ɋ����đo���`���������ɗ��܂������A����Ő��w�I�ȑΏ̑���ɋ����āA���Ⴊ�Ȃ��Ă��\���̂���V�����`�����������������w�ҁi���w�ҁj�������������B
�t�����X�̃W�����W���E�t���[�f��(Georges
Friedel:1865-1933)�͂��̈�l�ł���B�p���z�R�w�Z�̃}���[���̉��ōz���w���w�сA�T���E�G�`�G���k�̍z�R�w�Z�ŋ��ڂ��Ƃ����B�ꎟ����̓X�g���X�u�[���Ɉڂ����B�����̈�͑���ɏ邪�A���܂��܂ȕ�����l�H��������Ȃ��ŁA�o���ɂ��ĖL���Ȓm�����������B�S�[���h�V���~�b�g�̑o����`�܂��A�������̐V�����`����\�������B���̂����A(2021)��o���ʂƂ���X�����A�y��
(2131)��o���ʂƂ���X�����Ƃ́A��ɍ��������Ŏ��Ⴊ���ꂽ�B
�܂��K���f�b�g���i���{���j�Ɏ����X��
90�x�̑o�������������Ɍ��o���ĕ����B�S�[���h�V���~�b�g�͔ے肵�����A�V���f���͗L���ƍl���A�u�t���[�f���̒������v�ƌĂB�V�R�����ɂ����������B
���Ȃ݂Ƀt���[�f���� 600���̕��͋C���Ő����ɐ������H�����������āA�����������Z�����n�ł��邱�Ƃ𐄘_���Ă���(1902�N�j�B
�@
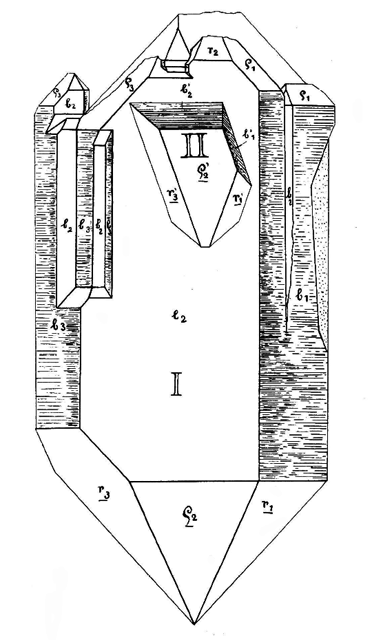
F.�V���f�� "Quarzzwilling nach dem Zinnwalder Gesetze
von Crapteig (Viamala), Graubiinden"(1912)���
�@�u�`�������h���o���v�̕W�{��
�i�O���E�r�����f���ACrapteig�Y
�W�{�����S�b�V���瓾���W�{�j
����̌́i�T�j�̒��ʂƁA�����i�U�j��
���ʂƂ����s�ɂȂ�^�C�v
�T�̃T�C�Y 5.3x2.5cm
�T�ƇU�Ƃ͓���łȂ��B
���t�H���`���i�[�g�E�V���f���i�c�B���f���j(Fortunat Zyndel:
1882-1917)�̓X�C�X�̒n���E�z���w�҂ł���B1910�N��i�ꎟ���O�j�ɂ͎�Ƀo�[�[���̍��Z�ŋ��ڂ��Ƃ�T��A�o�[�[����w�ŕ����w�A���w�A�z���w�Ȃǂ̌��������Ă����B1909�N�ɐ����̐V�����o���`���Ɖ~�Ό��Ɋւ��錜�ܘ_���ɉ��債�A�s�G�����e�n���u���b�\���Y�̓��{���i�K���f�b�g���j�o���ɂ��Ę_�����B�ȗ�������i�߂āA���̕���̓��カ���Ă̐��ƂƖڂ����悤�ɂȂ�B
V.�S�[���h�V���~�b�g�ƕp�ɂɌ�M���A�ނ̂���n�C�f���x���N�ɗ��Ċ������邱�Ƃ����߂�ꂽ���A�o�[�[���ɗ��܂����B�x���M�[��
J.�h���O�}��(��ɍ����Ήp�̂��܂��܂ȑo���`�������)��A�����̌����҂Ƃ��ڐG���������B
1912�N�ɔ��\�����u�����̌X�����i�厲�s���j�o���ɂ��āv(Über Quarzzwillinge mit nichtparallelen
Hauptachsen)�Ŕ��m�����B�ނ̈�A�͈̕�ʂ̍z�����Ђł͖������ꂪ���ȓ��{���ȊO�̂��܂��܂ȌX���`���Ɍ��y���Ă���A�S�[���h�V���~�b�g�̌����u�K���I�Ȗ����v�i�ɉ߂��Ȃ����́j���A���ۂɌ����\����̔z���ɏ]���o���ł��邱�Ƃ��A�����̎���𑍍��I�ɒ��邱�Ƃŗ�����Ӑ}���������i���{���ȊO�̌`��������/�����m���ɖR�������̂ł��邱�Ƃ�F�߂��j�B�܂��\���̂���i���ᖢ�́j�`�����������w�E�����B
1912�N�̕ŃV���f���͌X�����o���� 12�̌`���𐔂��A���̂��� 11�ɂ��Ď���/�����o���Ă����i��������
12�Ԗڂ̓[�[�h���t�U���j�B
1913�N4���t�̕ł� 3�̉��������܂� 16�`���������A����
4�O���[�v�ɕ��ނ����B
I. ���̂̓���̒��ʓ��m�����s�ɂȂ�O���[�v�@(Deckung
von b2 mit b2�f)
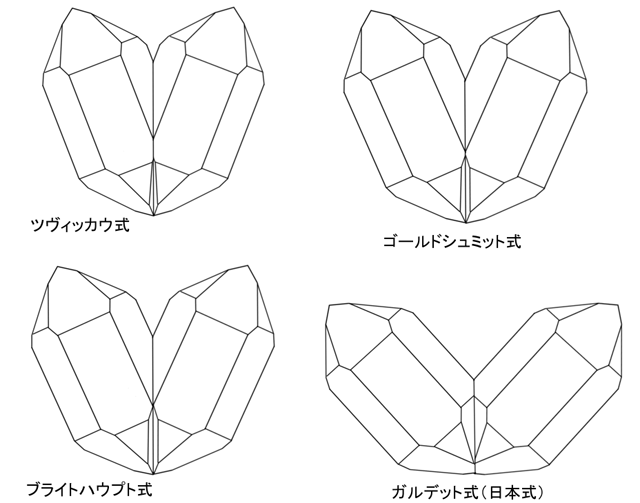
�@1. �c�r�b�J�E�� �iG.�C�G���V���j
�@2. �S�[���h�V���~�b�g���@�iV.�S�[���h�V���~�b�g�j
�@3. �u���C�g�n�E�v�g�� �iA.�u���C�g�n�E�v�g�j�@ (2�� 3�Ƃ͓�d�ɓ����ĂЂƂ̌X�������Ȃ��ƃV���f���͍l����)
�@4. ���{���@�iC.S.���C�X�j
�@5. �t���[�f���̒������@�iG.�t���[�f���j
II. ���̂̓���̐��ʓ��m�����s�ɂȂ�O���[�v (Deckung von r2 mi r2�f)
�@6. �����`�i�G�[�j���@�i��̃V���f���`���j�@�iF.�V���f���j
�@7. �T���W�j�A���@�iQ.�Z�b���j
�@8. ���� ��(![]() )�i�A�[�j���@�iF.�V���f���j
)�i�A�[�j���@�iF.�V���f���j
�@9. ���C�w���V���^�C���E�O���[�[�����^�[�����@�iG.���[�[�AV.�S�[���h�V���~�b�g�j
III.
����̌̂̓���̐��ʂƑ����̓���̒��ʓ��m�����s�ɂȂ�O���[�v
(Deckung von b2 mit r2�f)
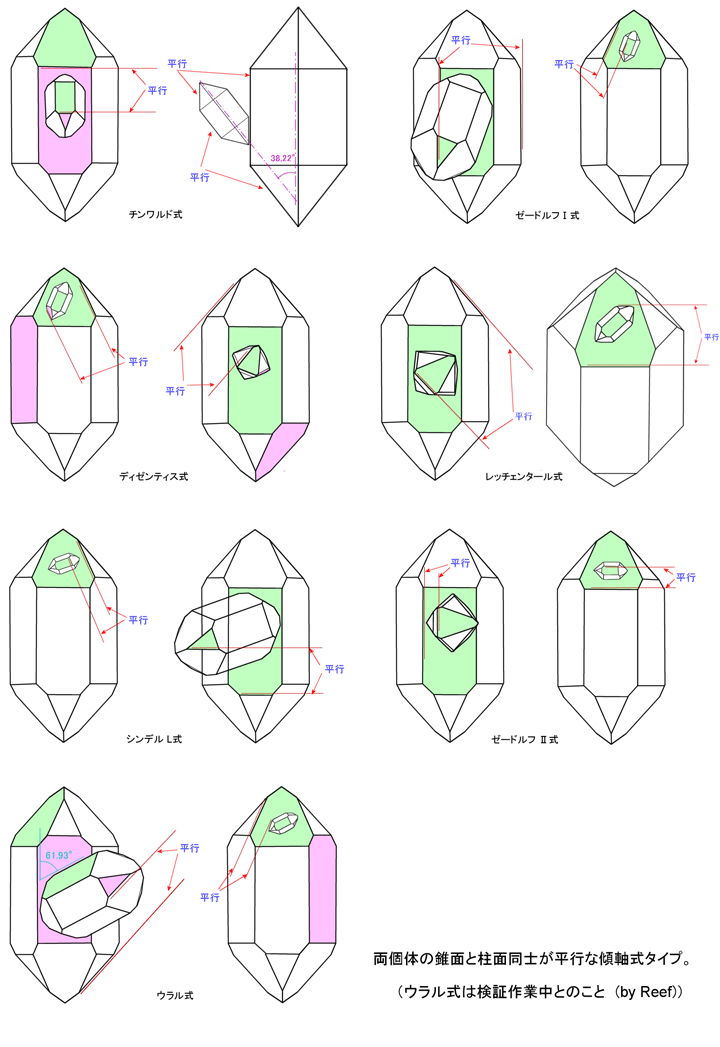
�@10. �`�������h���@�iG.�C�G���V���j�@
�@11. �[�[�h���t �T�� �iF.�V���f���j
�@12. �f�B�[���e�B�X���@�iF.�V���f���j
�@13. ���b�`�F���^�[�����@�iF.�V���f���j
�@14 . L���i��̃V���f�� L���j�@�iF.�V���f���j
�@15. �[�[�h���t�U���@�iF.�V���f���j
IV.
����̌̂̏��сi�]�[���j���A�����̈قȂ鏻�тɑΉ�����O���[�v
(Deckung von Zonen mit Flächen b, r, �� mit Zonen ohne diese Flächen)
�@16. ����R���@�iF.�V���f���j
�ȏ�� 16�`���̂��� 8�� (1�A2�A3�A4�A5�A7�A9�A10)��
�V���f���ȑO�Ɋm�F����Ă������̂ŁA���� 5�� (11�A12�A13�A14�A15)�̓V���f����������������������̂ł���B�ނ͂܂����̎��_��
3�� (6�A8�A16)�̉�����������B���Ȃ킿�����ɂ����� 8����V���ɉ������킯���i���ŕW���j�B
�O���[�v�T�`�V�́A����̌̂̏��сi���s�ʌQ�j b, r, �ς������̓������тɌĉ����邱�ƂŁA�����w�I�ɑo���Ɗm�F�o������́B�V���f���͂��̑��ɁA����̏���
b, r, �ς������̈قȂ鏻�тɌĉ�����^�C�v�̉\����z�肵�A�����I�ɃO���[�v�W�i����R���j��݂����B
�O���[�v�V���́A�[�[�h���t�A�f�B�[���e�B�X�A���b�`�F���^�[���̖��̂̓X�C�X�̒n���ŁA�����Y�n�̕W�{��������钆�ŁA���ꂼ��̎���������̂������B
�[�[�h���t I �� 1910�N�ɃV���f�����\������ 3�`���̈�ŁA1912�N�܂łɃE�����[�[�h���t�Y�ɂ���Ċm�F���ꂽ�B1913�N�ɂ̓[�[�h���t�U�̊m�F���Ƃ�Ă����悤���B
�V���f���k�����܂��[�[�h���t�Y����m�F���ꂽ�i����łȂ��j�B
�f�B�[���e�B�X���́A�V���f�����`�������h�����m�F�����f�B�[���e�B�X�Y�W�{�Ɉꏏ�Ɋ܂܂�Ă����V�`���B�`�������h���Ɏ��Ĕ�Ȃ���́B
���b�`�F���^�[�����́A�ŏ��̎���� Solothurner
�����َ����̃��b�`�F���^�[���Y�W�{�ɋA���B�V���f���̓[�[�h���t�Y�̕W�{
3�P�ɂ����̎������o�����i����łȂ��j�B
1913�N�̌̕���V���f���ɂ͑o���̌����𑱂���]�݂��������B�Ⴆ�Γ��{���o���ł͐ڍ����E�t�߂ɓ��������\���ُ̈킪���邱�Ƃ��ώ@���Ă���A���̌�����[�߂邱�ƂŔz���I�Ȗ����̋@�\�����炩�ɏo����Ɗ��҂��Ă����B���A�ꎟ��킪�N�������B1917�N2���ɉp���D�D���R�j�A���Ńj���[���[�N���烊�o�v�[���Ɍ��������V���f���́A�A�C�������h���Ńh�C�c�����͂̍U���������R�j�A���Ƌ��ɏ����������B
�@
�܂Ƃ�
���t�����f����Dana 7th (1963)�ő����I�Ɏ����� 15�̌X�����o�������M�������[ No.1007�ɏЉ�����A�ȏ㌩�Ă����ʂ�A�`�t���X���i���V���f���`���ɗގ�/�X������p�W�j������ 13���܂ł��V���f���ɂ���ċL�ڂ���Ă���(�����̃V���f���`�����܂߂��14��)�B�t�����f���� 3�̃O���[�v�������V���f���̂���ɕ���Ă���B
�ȉ��Q�l�܂ł� Dana 7th �́A���{���ȊO�� 14�`���ɂ��Ẵe�L�X�g����������B�i�]�[���ɂ��Ă̋L�q�͎��ɂ͂悭������܂��B�j
�w���ׂĂ̌`���͑o�������̓��m�̍��W�n�� a���̋ɐ��ƍ��E��ɂ���ĕ��ނ��邱�Ƃ��o����B�����̑o����zonal relation�̋L�q�ɗp���錋���ʂ̃V���{���̓V���f�����̑��̒��҂炪�X�����o���ɗp������`�ɏ]���B
�Q�D�c���B�b�J�E���F ���ʓ��m���R�v���[�i�[�B�����X�� 42��17'�B
�i����́j�ub1b2b3�� ��1b2r3�v�̖ʂ��Ȃ��]�[���ƁA�i�����́j
�u��1b2��3��b1b2b3�v�̖ʂ��Ȃ��]�[���Ƃ��A�o���ɂ����ĕ��s�B���Y�n�̓U�N�Z���̃c���B�b�J�E�B�X�C�X�̃[�[�h���t�A�f�B�[���e�B�X�AFinsteraarhorn
�ɂ��Y����B
�R�D�S�[���h�V���~�b�g���F�@���ʓ��m���R�v���[�i�[�B�����X�� 47��43'�B�ur3b2��1��b2r2o�v�̖ʂ��Ȃ��]�[���ƁA�ub2r2o ��r1b2��3�v
�̖ʂ��Ȃ��]�[���Ƃ��o���ɂ����ĕ��s�B�s�G�����e�̃u���b�\���Y�A�t�����X�̃h�[�t�B�l�Y�i�H�j�ɕB
�S�D�u���C�g�n�E�v�g���F�@�o���ʂ� (1121)
�B�o������̌Q�͓�̃R�v���[�i�[�Ȓ��ʂ������A�����X�� 48��54'�B�ub1r2��3��b3��2��1�v�A�y��
�ub3��2r1�� b1��2r3�v�̃]�[���Ƃ����s�B�h�[�t�B�l�ƕs���Y�n����B
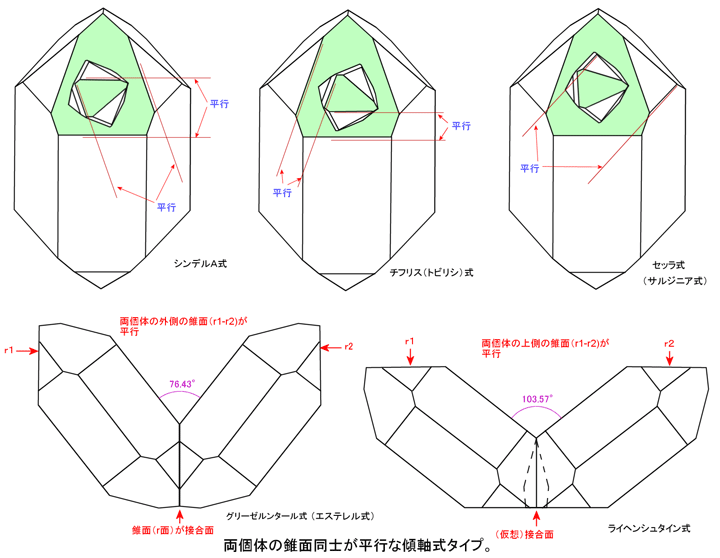
�T�D�t���[�f���̒������F�@��̃R�v���[�i�[�Ȓ��ʁA�����X�� 90���B(44-81)�ʏ� ��45��39'��]�̑o���Ƃ��\���B���������Ŋώ@�����B�V�R�ɂ���̕s���Y�n����A�X�C�X�ɎY����Ƃ��B
�U�D���C�w���V���^�C���E�O���[�[�����^�[�����F�@(1011)���o���ʁB�����X�� 76��26'�B��]�p180���B�ub2r2o ��
b2r2o�v,�ub1r2��3�� b1r2��3�v,�y�сub3r2��1��b3r2��1�v�̃]�[�������s�B�����̗�̓U�N�Z���̃��C�w���V���^�C���Y�ȂǁA�����͂̂��ɕ����(0112)�ʂő��ʕ����ɐڍ������[���o���ł��邱�Ƃ������ꂽ�B
���̌�X�C�X�̃O���[�[�����^�[����S�b�V�F�i�[�A���v�Y�̂��̂ŕ��ꂽ�B���������̃G�X�e�������o���Ɠ��ꎮ�̂��́B
�V�D�Z�b�����F�o���� (1012) ��]�p 86��4'�B
�����X�� 64��50'�B�� �ub3��3o�v�Ɓub1��4o�v�Ƃ����s�B�ŏ��ɃT���W�j�A�Y(?)�ŕB���̗Ⴊ�����������ቷ�������s���B�n���K���[�̃}���}���V��������B�����Ήp�̃T���W�j�A���Ɠ��ꎮ�B
�W�D�V���f��A���F �o1011�p�̓�̕H�ʑ̖ʂ��R�v���[�i�[�B��]�p 70��21'�B
�ub1r2��3��b2r2o�v�A�y�сub2r2o��b3r2��1�v�̃]�[���Ƃ��o���ɂ����ĕ��s�B�X�E�F�[�f���̃w�b�Z���N�b���Y�A�n���K���[�Y�̂Q��B
�X�D�`�t���X Tiflis ���@(�V���f��A) �F(1011)�̓�̕H�ʑ̖ʂ��R�v���[�i�[�B��]�p 109��39'�B�ub3r2��1��b2r2o�v�A�y�сub2r2o��b1r2��3�v�̃]�[���Ƃ��o���ɂ����ĕ��s�B�g�����X�R�[�J�T�X�̃`�t���X�i�g�r���V�j�Y�B
�P�O�D�`�������h���F�@�e�̂̈��(1011)�H�ʑ̂����̂̒��ʂɕ��s�A��̃Z�b�g���ڐG���āA������(1120)�ʂɉ����Ċp�x38��13'�Őڍ��B��]�p 0���B�U�N�Z���̃`�������h����A�X�C�X�̃f�B�[���e�B�X�A���B�A�}���A�V�����X������B�X�E�F�[�f���̃I�t�F���_���A�t�����X�̃h�[�t�B�l�A�č��̃g�����g���E�t�H�[���A�m���E�F�C�̃X�i�����A�n���K���[�Y�B
�P�P�D���b�`�F���^�[�����F���(1011)�H�ʑ̂����̂̒��ʂɐڐG�A��]�p
47��43'�B�ʁur3b2��1�v�Ɓuo��2b2�v�̃]�[���Ƃ��o���ɂ����ĕ��s�B�X�C�X�̃��b�`�F���^�[���A�f�B�[���e�B�X�A�[�[�h���t�Y�B
�P�Q�D�V���f��L���F�@���(1011)�H�ʑ̂����̂̒��ʂɐڐG�A��]�p 70��21'�B�ʁub2r2o�v�Ɓur1��2b3�v�̃]�[���Ƃ��o���ɂ����ĕ��s�B�X�C�X�̃[�[�h���t����P��B
�P�R�D�[�[�h���t I ���F�@���(1011)�H�ʑ̂����̂̒��ʂɐڐG�A��]�p 19��39'�B�ʁub1b2b3�v��
�ub1��2r3�v�̃]�[���Ƃ��o���ɂ����ĕ��s�B�[�[�h���t����P��B
�P�S�D�[�[�h���t II ���F�@���(1011)�H�ʑ̂����̂̒��ʂɐڐG�A��]�p 90���B�ʁub1b2b3�v�Ɓuo��2b2�v�̃]�[���Ƃ��o���ɂ����ĕ��s�B�[�[�h���t����P��B
�P�T�D�f�B�[���e�B�X���F�@�e�̂̈��(1011)�H�ʑ̂��A���̂̒��ʂɕ��s�ŁA��̃Z�b�g���ڐG�B��]�p 22��38'�B�ʁur1b2��3�v�Ɓur1��2b3�v�̃]�[���Ƃ����s�B�X�C�X�̃f�B�[���e�B�X����P��x
�� Dana 7th
�̋L�q�͌����w�̒m���ɖR�����҂ɂ͓���ŁA���ꂼ��̑o�����̃C���[�W��͂ނ��Ƃ�����B
�K���C���^�[�l�b�g��ɂ́A���݂̂Ƃ���A�u�z���̗F�t�H�[�����iFMF:
Friends of Minerals Forum�j�v�ɂ����āA "Rarest quartz twins with inclined axes C"�i�����Ƃ������������̑o���A�b���̌X�������́j�Ƃ����f�����A�N�e�B�u�ŁA������
Reef
�Ƃ����n���h���l�[���̕����A�e�`���̑o���̓����ƌ����}�A�����Ď���W�{�̉摜�Ƃ��f�����Ă�����B
�����̂�����͌������āA�����ɂȂ�ꂽ���B
Reef �����܂� Dana 7th �̋L�q�ɐڂ��ē����͓V�����ꂽ���������B�����d�˂āA���ꂼ��̃C���[�W�}��`�悳���܂łɂȂ�ꂽ�R�B��L�̌`���̂قƂ�ǂ�������Ă���A�܂��Ǝ��Ɍ�������Ă���炵���A�u�E�������v�̏����ڂ��Ă�����B
���Ȃ݂Ɉȉ��̐}�́A Reef ���̌����}�����~���� sps����̕ҏW�����������̂ɂȂ�B��������Q�l�܂Łi�I���W�i�����Ƃ��Ă�
Reef ���̍�}�ɒ��ړ������Ă������������j�B
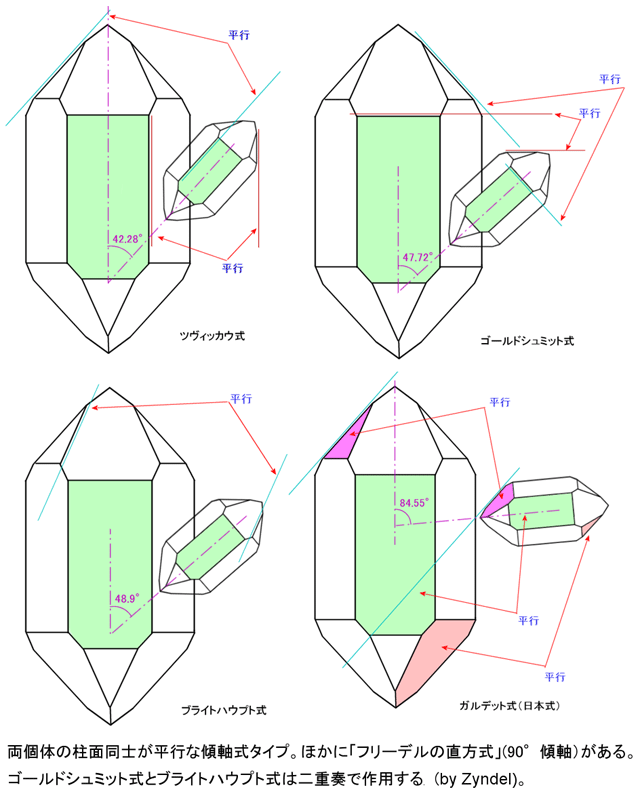
(�����j�@���̂S�@(J.Drugman �̕ɋL���ꂽ���������̌X�����o���ɂ���